CAPM模型，即资本资产定价模型，是现代金融理论的重要组成部分，该模型由威廉·夏普等人于上世纪六十年代提出，主要用于描述资产的预期收益率与风险之间的关系，CAPM模型的推导基于一系列假设和理论，如市场有效性假设、投资者理性假设等，本文将详细介绍CAPM模型的推导过程，并探讨其在实际应用中的价值。

CAPM模型的推导

CAPM模型的推导基于以下基本假设：

1、市场有效性假设：市场中的投资者都是理性的，他们能够根据资产的风险和预期收益做出最优投资决策。

2、投资者理性假设：投资者对资产的预期收益和风险具有相同的看法，即市场具有一致性预期。

3、资产无限可分割性假设：资产可以无限分割，使得投资者可以投资于任何规模的资产组合。

4、无交易成本假设：投资者在买卖资产时无需支付交易成本。

基于以上假设，CAPM模型的推导过程如下：

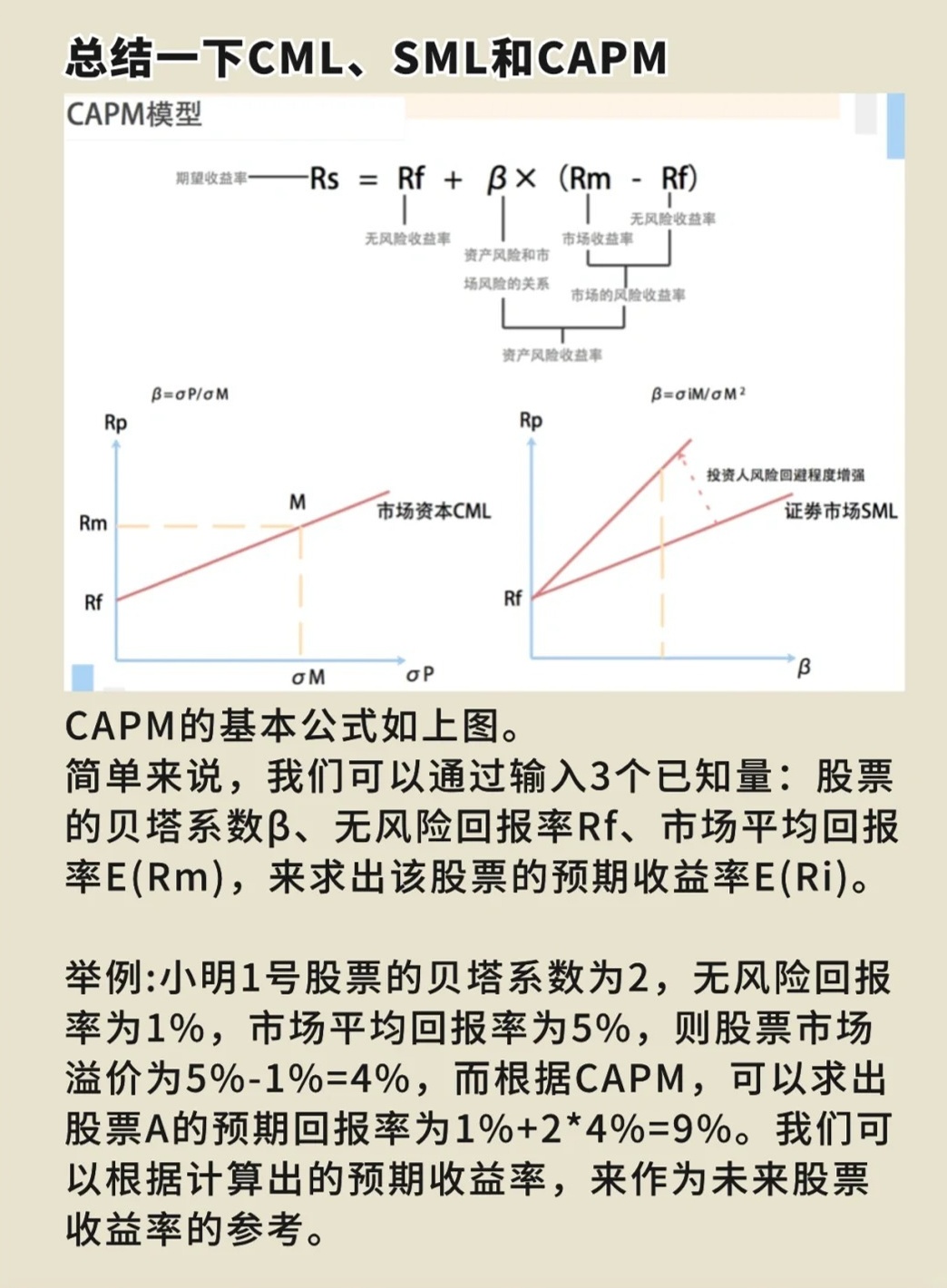
我们定义两个关键变量：资产的预期收益率（E(R)）和无风险收益率（Rf），预期收益率是投资者对资产未来收益的期望，无风险收益率是投资者在无风险资产上获得的固定收益，CAPM模型的目标是确定资产的预期收益率与无风险收益率之间的关系，为此，我们引入市场风险溢价的概念，即资产预期收益率与无风险收益率之间的差额，市场风险溢价反映了投资者承担额外风险所获得的补偿，根据CAPM模型，市场风险溢价与市场贝塔系数（Beta）成正比关系，Beta系数衡量了资产的系统风险（即市场风险），而非特定公司的特有风险，Beta系数越高，意味着资产的系统风险越大，投资者要求的补偿也越高，CAPM模型的数学表达式为：E(R) = Rf + β * [E(Rm) - Rf]，其中E(Rm)表示市场投资组合的预期收益率，这个公式描述了资产的预期收益率与其Beta系数之间的关系，当Beta系数为1时，资产的预期收益率等于市场投资组合的预期收益率；当Beta系数大于1时，资产的预期收益率高于市场投资组合的预期收益率；当Beta系数小于1时，资产的预期收益率低于市场投资组合的预期收益率，这就是CAPM模型的核心思想，通过调整Beta系数的大小，我们可以预测不同资产的预期收益率，CAPM模型还可以用于分析投资组合的风险和收益，通过将不同资产的预期收益率与市场投资组合的预期收益率进行比较，我们可以计算出投资组合的预期收益率和风险水平，这为投资者提供了重要的决策依据，帮助他们制定投资策略和优化投资组合，在实际应用中，CAPM模型还可以用于评估基金经理的投资表现和市场效率等，通过比较实际收益与CAPM模型预测的收益，我们可以评估基金经理的投资能力及其对风险的把控能力，通过观察市场收益率与CAPM模型预测值的差异，我们可以判断市场的有效性程度和市场效率水平，CAPM模型的推导过程基于一系列假设和理论，通过引入Beta系数和市场风险溢价等概念来描述资产的预期收益率与风险之间的关系，在实际应用中，CAPM模型为投资者提供了重要的决策依据和投资分析工具，有助于他们制定投资策略和优化投资组合，三、CAPM模型的应用价值CAPM模型在现代金融领域具有广泛的应用价值，它为企业和投资者提供了评估投资风险和收益的工具，通过计算资产的Beta系数和预期收益率，企业和投资者可以更好地了解投资项目的风险和收益水平，从而做出更明智的投资决策，CAPM模型为投资组合管理提供了重要的指导，通过优化投资组合的资产配置，投资者可以降低整体投资风险并寻求更高的投资回报，CAPM模型还可以用于评估基金经理的投资表现和市场效率等，通过观察实际收益与CAPM模型预测值的差异，我们可以评估基金经理的投资能力和市场效率水平的变化情况，CAPM模型对于金融教育和学术研究也具有重要意义，它为学生和研究者提供了深入理解金融市场和资产定价机制的机会，有助于推动金融理论的发展和创新，CAPM模型的应用价值体现在多个方面，包括投资评估、投资组合管理、市场效率分析和金融教育等，四、结论通过本文的阐述可以看出，CAPM模型是现代金融领域的重要工具之一，它基于一系列假设和理论进行推导，通过描述资产的预期收益率与风险之间的关系为投资者提供决策依据和分析工具，在实际应用中，CAPM模型具有广泛的应用价值包括投资评估、投资组合管理、市场效率分析和金融教育等，然而需要注意的是任何模型都有其局限性在应用过程中应结合实际情况进行综合考虑和分析以便做出更明智的决策总之通过深入研究和实践应用我们可以更好地发挥CAPM模型的价值为现代金融领域的发展做出更大的贡献。